Tableauの公式ヘルプの関数の項目には掲載されていませんが、TableauにはRANDOM()という関数があります。公式には認めていない関数ということで、いわば「隠し関数」になっています。
以下が計算フィールドでRANDOM()を使ったものです。フィールドの左側下部に「計算は有効です」とありますので、計算式として成立しているのが確認できます。
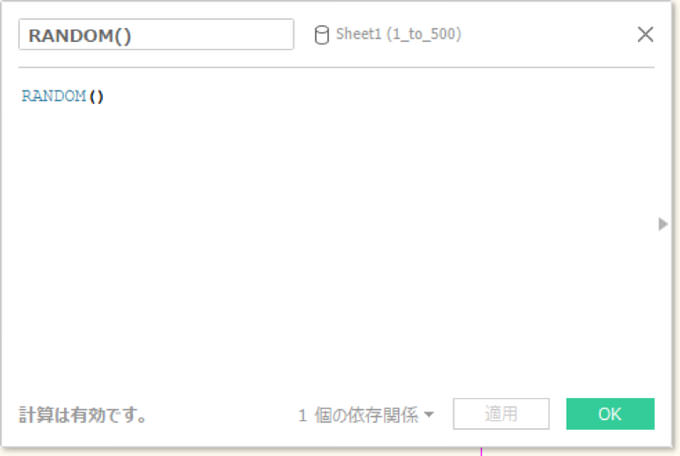
以下が、行ID(1から1500)に対して、RANDOM()を「 円」で表現したものです。きれいに乱数が出ているように見えます。
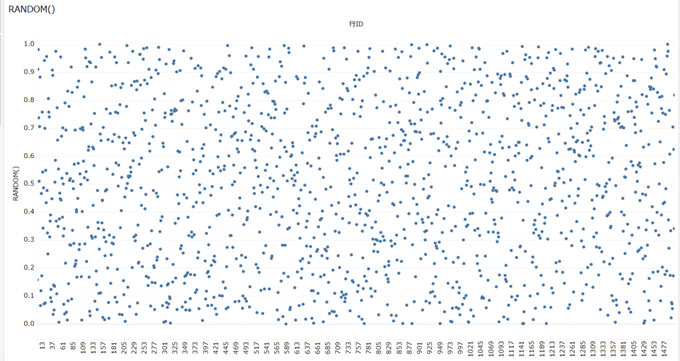
一方、以下の記事を参照すると数学的な「乱数」はそんなに単純なものではないことが分かります。
あなたの使っている乱数、大丈夫?
-危ない標準乱数と、メルセンヌ・ツイスター開発秘話-
松本 眞
広島大学理学研究科数学専攻
2014/11/18, 第50回市村学術賞記念 先端技術講演会
http://www.math.sci.hiroshima-u.ac.jp/~m-mat/TEACH/ichimura-sho-koen.pdf
つまり、「乱数」を得るには、「一様かつ独立に次々とでたらめな数を発生させる方法」乱数発生法が必要ということです。
「でたらめ」でなければいけないので、特定の数への集中や、繰り返しがあってはいけないということになります。
「でたらめ」でないと、以下のような問題が起きる。ということですね。

一方、上記の講演資料にも、乱数を説明したWikipediaにもありますが、重要で、どうしても理解しておかなければいけないのは、「決定的動作しかしない計算機(=コンピュータ)では乱数は生成できない」ということです。つまり、コンピュータは、ある計算をして解を求める(=決定的動作をする)ことしかできず、本当の「偶然」や「でたらめ」は作り出せないということです。
では、サイコロやルーレットのような(それでも重心の偏り等で本当に「でたらめ」かどうかは議論があると思いますが)「物理乱数発生器」を使えばよいのか。と考えるのですが、その場合「再現不能性」という問題があります。
つまり、ある計算をするときに「でたらめ」な数である必要がある一方、その計算を検証するために毎回、誰がやっても取り出せる「同じでたらめな数」が必要だ。ということです。
TableauのRANDOM()については、公式ナレッジベースで「RANDOM() 関数による一貫性のない結果の生成」として説明がありますが、それは「再現不能性」がある。ということを意味していると思います。
確かに、Tableauで作成したVizはF5で再読込を行うと、値が変わってしまいます。そして二度と同じ”乱数”を発生させることはできません。
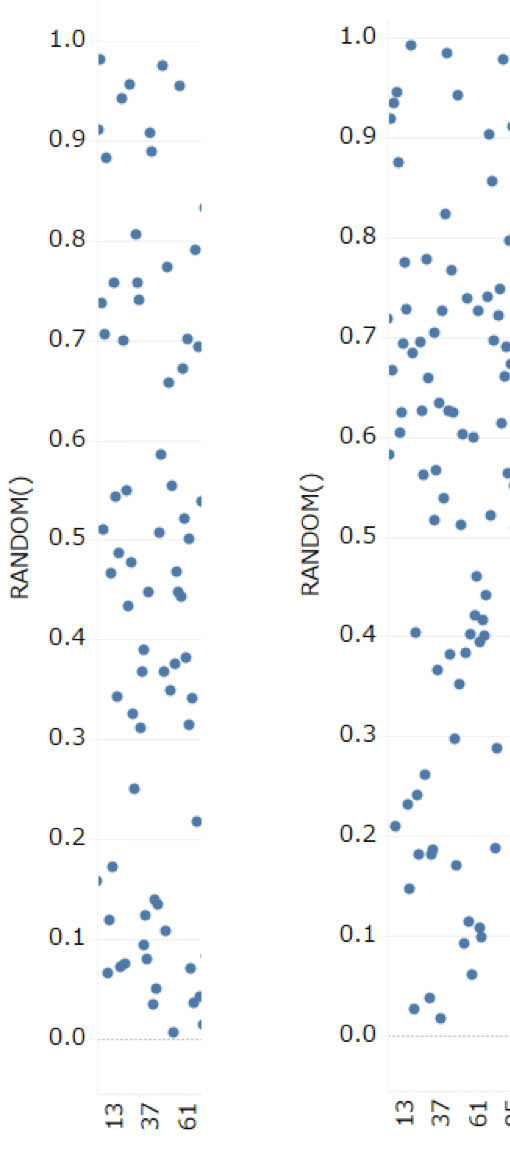
そこで登場するのが、「かなりでたらめ」であり、かつ「再現性がある」性質を持つ、「擬似乱数」です。以下が擬似乱数についてのWikipediaからの引用です。
擬似乱数(ぎじらんすう、pseudorandom numbers)は、乱数列のように見えるが、実際には確定的な計算によって求めている擬似乱数列による乱数。擬似乱数列を生成する機器を擬似乱数列生成器、生成アルゴリズムを擬似乱数列生成法と呼ぶ。
真の乱数列は本来規則性も再現性も無いものであり、その定義から、確定的な計算によって求めることはできない(例:サイコロを振る時、今までに出た目から次に出る目を予測するのは不可能)。一方、擬似乱数列は確定的な計算によって作るので、その数列は確定的である。また、生成法と内部状態が既知であれば、予測可能でもある。
ある擬似乱数列を、真の乱数列とみなして良いかを確実に決定することはできない。
という訳で、前振りが長くなりましたが、今回の記事は、Tableauの計算フィールドを利用した「擬似乱数」を発生させる方法を解説します。
Tableauでの疑似乱数発生させる方法論
いろいろと調べ、こちらの線形合同法を利用することにしました。

modとは、割った「余り」を求めるので、ものすごく乱暴にいうと、0より大きいある定数(A x Xn+B)をAよりも大きい定数Mで割った余りを使います。さらに、最初の計算で取り出した余りを次のXnとして使います。
線形合同法ではこの Xnのことを「乱数の種」としています。

Tableauの計算フィールへの実装は、ページの下部に記述があった、Park & Millerの方法でやってみます。

もうお分かりと思いますが、上記では、「乱数のたねと48271を掛けた数」を、「2の31乗マイナス1」で割った余りを取り出しています。
Tableauでの疑似乱数発生させる計算フィールド
Tableauで以下の計算フィールドを作りました。
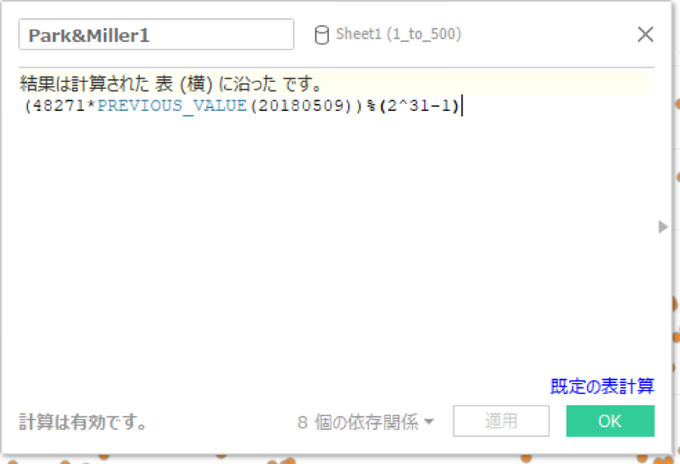
乱数の種として、執筆している日を使いました。ま、なんでも良いので。
ただ、この種を定数とすることで、再現性が生まれるので、その観点では重要です。
また、以下の通りに、種を変えてPark&Miller2を作成し、、、
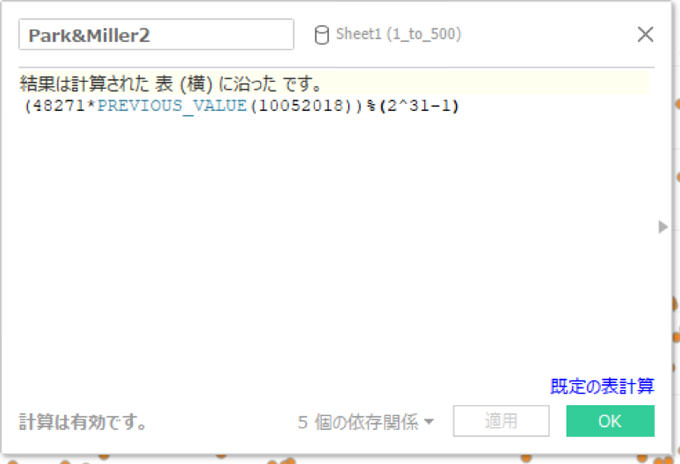
散布図にしたのがこちらです。
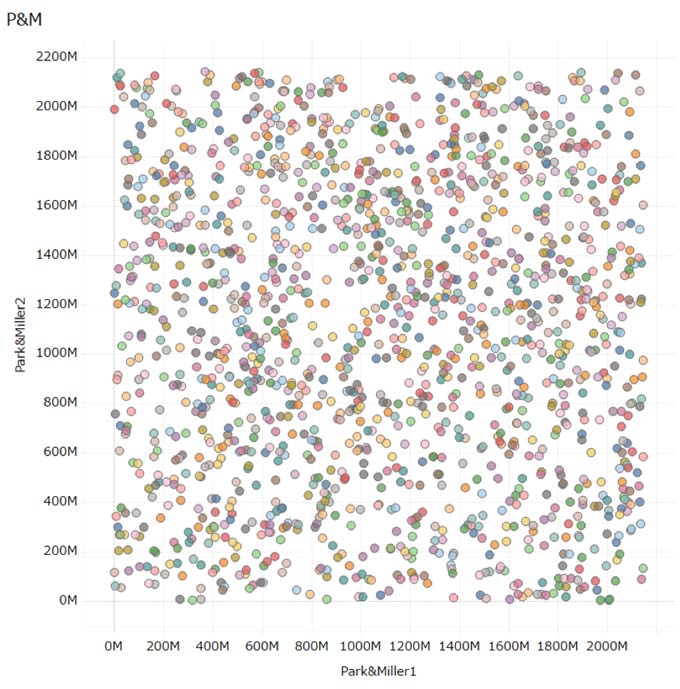
程よく散らばっているように思います。これで、「かなりでたらめ」でかつ、「再現性がある」疑似乱数をTableauで発生させることができました。
TableauでRANDBETWEENのような一定の範囲の疑似乱数を生成する
次にTableauでRANDBETWEENのような一定の範囲の疑似乱数を生成したいと思います。
RANDBETWEENとはエクセルに用意されている関数で、指定した範囲の疑似乱数を作成するものです。
RANDBETWEN(1,100)
とすれば1から100の間の疑似乱数が得られます。ただ、RANDもRANDBETWEENも、「乱数の種」は使わないようなので、TableauのRANDOM()と同様再現性のない疑似乱数であるように思えます。
Tableauで決まった範囲の疑似乱数発生を実現するには、以下の計算式を使います。
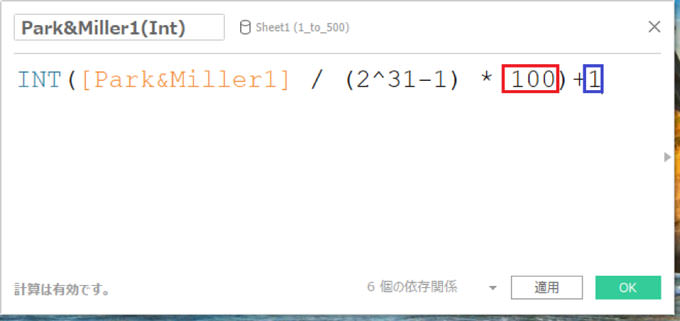
- 青枠は取り出したい疑似関数の最小値です。
- 赤枠はいくつの乱数を欲しいか?を定義します。
したがって、上記の例では、1から、整数で100個、つまり、1から100までの疑似乱数を取り出す事ができます。サイコロのように1から6までを欲しいのであれば、
青枠は1、赤枠は6とします。
結果は、以下となります。
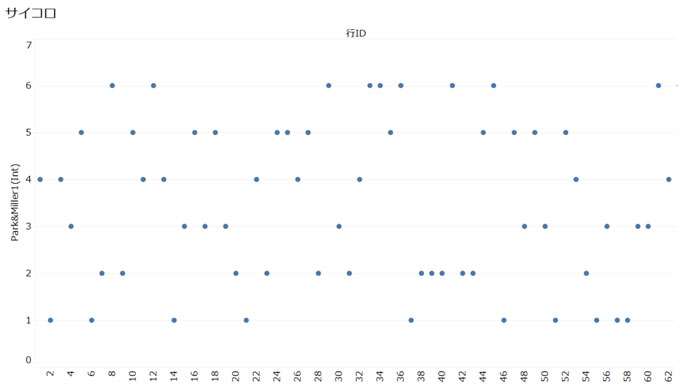
ちゃんと、1から6までの疑似乱数が取り出せていますね。少数が欲しい場合には、全体を0.1や0.01で割るなどで対応可能です。
Tableau PublicにVizをパブリッシュしていますので、興味ある方は、ダウンロードしてリバースエンジニアリングしてみてください。
https://public.tableau.com/profile/kazkida#!/vizhome/random_in_tableau/PM
まとめ
RANDOM()がなぜ、公式に認められた関数ではないのか?を調べているうちに、コンピュータによる乱数の発生の課題を学び、それをできるだけ上手に解決する方法として、疑似乱数発生装置としてのPark&Millerにたどり着き、最後はそれを利用してTableauで疑似乱数を発生させることができました。
プリンシプルでは、Tableauによるデータの可視化をサービスとして提供しています。ご興味を持たれた方はinfo@principle-c.comからお気軽にお問い合わせください。








