今回はマーケティングの分析にも使用される、統計的仮説検定のロジックについてお話します。
統計的仮説検定はグーグル広告のキャンペーンテストにも使用されています。その際登場する、「統計的に有意」「P値」「有意水準」などの用語に混乱している方も多いのではないでしょうか?
そんな統計の知識に不安のある方に向けて、今回は統計学の用語をなるべく使わずに統計的仮説検定のロジックを説明します。
記事の内容
- 統計的仮説検定は「偶然か否か」を見極める統計学的なアプローチ
- 【解説】統計的仮説検定のロジック
- 統計学の用語を使うと
- 判断を間違うこともある
統計的仮説検定=「偶然か否か」を見極める統計学的なアプローチ
サイト解析や、広告運用、マーケティングの世界で日々、色々なデータを見ますよね。その際データ同士の差を見ることはが多いのではないでしょうか?
例えば、あるサイトのコンテンツの訪問ユーザー数について、男性が550、女性が450だったとしましょう。一見すると「男性が多いな、男性に支持されているコンテンツなのでは」と感じるかもしれません。
しかし、そのデータについて、上司やクライアントに報告したとき次のように言われたらどうでしょうか?
「偶然じゃない?」
うーん。確かに。偶然かもしれません。でも本当は意味のある差なのかもしれません。
一体どのような根拠をもとに説明をすればいいのでしょうか?「男性に支持されているコンテンツ」なのでしょうか?それとも「偶然男性が多かっただけ」なのでしょうか?
このような偶然起こった事象か否かを定量的に見極める方法が統計的仮説検定です。
【解説】統計的仮説検定のロジック
問題設定:コイン投げの例
突然ですが、私とコイン投げをしたとします。オモテが出れば私の勝ち、ウラが出ればあなたの勝ちの10回勝負です。
通常、コインがオモテになる確率、ウラになる確率どちらも50%です。どちらが勝利しても偶然といえるでしょう。きっと6対4くらいの良い勝負になるはずです。
しかし、結果は10対0で私の圧勝。これは偶然の結果でしょうか。あなたはコインに仕掛けがしてあるのでは?と疑うのではないでしょうか。
偶然かどうかは確率で見極める
確かに、私はコイン投げの勝負で不正をしているかもしれませんが、一旦頭を冷やして考えてみましょう。
ここは、100歩譲ってコインには仕掛けがないと考えるのです。そうすると、以下のことが見えてくるはずです。
コインには仕掛けがない(=オモテが出る格率が50%)と仮定すると、10回コイン投げを行った場合オモテが出る確率は以下のようになります。
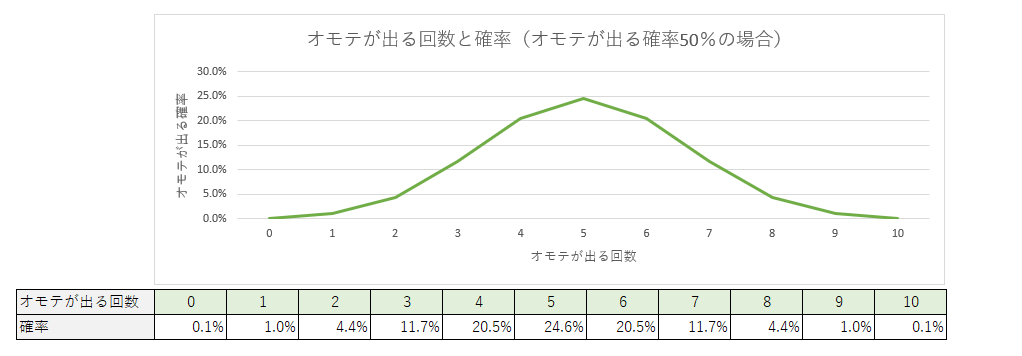
このグラフによると、10回オモテが出る確率は0.1%。つまりコインに仕掛けがない場合、私は、1000回勝負した時に1回起こる奇跡を起して勝利したことになります。
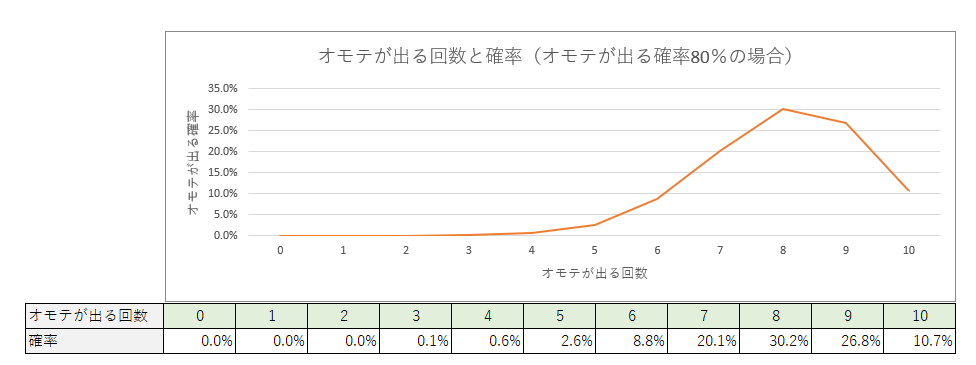
もし私がオモテが出る確率が80%になるような仕掛けをコインにした場合、10回オモテが出る確率は10.7%です。この場合には10対0というのは偶然起こりうる比較的自然な勝敗結果と言えるでしょう。
偶然の閾値を決める
私がコイン投げで10回中10勝する確率は、0.1%でとても低い確率であることが分かりました。しかし確率的に何%以上を偶然、何%以上を偶然ではないと考えれば良いのでしょうか?
この答えには、一般的な水準があります。統計学の世界では5%もしくは1%を水準に、確率が水準をを下回る場合、偶然ではない(=起こりえない)と考えます。
今回は5%を水準に考えてみましょう。
結局コインに仕掛けはしてあるのか?
ここまでの話を整理すると、「コインに仕掛けがしてある(オモテがでる確率が50%以上)」という疑いを「コインに仕掛けがしていない(オモテがでる確率が50%)」という仮設から検証してきました。
今回は、5%以上起こる事象については偶然(=良く起こる)と設定します。
すると、私がコイン投げで10回中10勝する確率は、0.1%(<5%)であることから、偶然でない(=起こりえない)と言えます。
ここで初めて、「コインに仕掛けがしていないという仮設(オモテがでる確率が50%)」は棄却され、「コインに仕掛けがしてある(オモテがでる確率が50%以上)」と疑うことができます。
つまり、統計的な根拠から、私の使用したコインのオモテが出る確率は、通常のコインとは違うと言えます。
統計学の用語を使うと
コインを10回投げるという例において、統計学の用語を持ち出すと以下のようになります。
- 「コインに仕掛けがしていない(オモテがでる確率が50%)」という仮説:帰無仮説
- 「コインに仕掛けがしてある(オモテがでる確率が50%以上)」という仮説:対立仮設
- 今回設定した閾値(5%):有意水準
- 私がコイン投げで10回中10勝する確率:P値
- 一連のプロセス:仮説検定
つまり、仮説検定とは、ある程度の確率を根拠として「帰無仮説」を棄却するか否かを判断すると同時に、「対立仮説」が正しいかを検証する事です。
判断を間違うこともある
コインに仕掛けがない場合、10回オモテが出る確率は0.1%と低い確率でしたが、確かに1000回勝負した時に1回起こることも事実です。
この場合、帰無仮説間違って棄却していまい、私はとばっちりを受けることになります。これを「第一種の過誤」と言います。
逆にコインに仕掛けがある場合でも、偶然妥当な勝敗結果になることがあります。
先ほどの2つのグラフを重ねて見ると、オモテが出る確率が80%のコインを使用したとき6対4で引き分ける確率は8.8%あります。オモテが出る確率が50%のコインの場合は20.5%。十分起こりえる確率ですね。
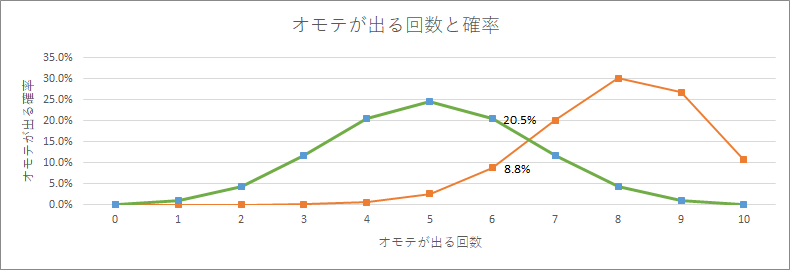
その場合帰無仮説が正しいにも関わらず、棄却できないことになります「これを第二種の過誤」といいます。
最後に
この記事では、統計的仮説検定のロジックを統計学の用語をなるべく使わずに解説しました。ロジックは理解いただけたでしょうか?
検定結果を確認する際にこのブログで紹介した内容を思い出してもらえると、より理解が深まるのではないかと思います。
また、弊社ではデータ解析を軸としたコンサルティングサービスを提供しています。是非こちらからご相談ください。