はじめに
独立性の検定と呼ばれる統計的仮説検定があります。
独立性の検定は、例えば、「投与した薬の違いは治癒率に関係しているか?」、「性別は安倍政権の支持率に関係しているか?」、「広告クリエイティブが違えば直帰率が異なるか?」など、
Aの要素がBに関係しているか?
を検定します。この検定に利用される検定手法が「カイ二乗検定」です。
検定の方法としては、Aの要素とそれぞれにおけるBの値から計算で求めたP値が0.05よりも大きければ「独立」、つまりAの要素はBには関係していない(「投与した薬の違いは治癒率に関係しない、性別は安倍政権の支持率に関係しない、広告クリエイティブの違いは直帰率に差を出していない」)となります。
逆にP値が0.05より小さいときは独立でない(「投与した薬の違いは治癒率に関係している、性別は安倍政権の支持率に関係している、広告クリエイティブの違いにより直帰率に差が出ている」)という結論となります。
エクセルによるカイ二乗検定 – データ
カイ二乗検定はエクセルでできますので、実際に手を動かしてカイ二乗検定のP値を求めてみましょう。
(同一広告グループからの)クリエイティブAとBについて独立性の検定を行います。目的変数は直帰率です。
データは以下の通りです。
クリエイティブA : 1,000セッションで直帰率50%
クリエイティブB: 1,200セッションで直帰率54%
セッションはどちらも1000を超えていて4ポイントの差があります。読者の皆さんは上記の差は「統計的に有意」だと思いますか?
エクセルによるカイ二乗検定 – 実際
① 基本的な表1
与えられたシナリオ通りに、以下の表をエクセルで作ります。

② 表の変形
次に、直帰したセッション、非直帰のセッションを取り出す用に変形します。太枠の「周辺度数」も計算します。(普通に行、列のSUM()です。)加えて、赤字の部分に、クリエイティブを問わない直帰セッションの割合(1,052/2,200)、非直帰セッションの割合(1,145/2,200)も記述します。この表が実測値(実際に観測された値)の表になります。
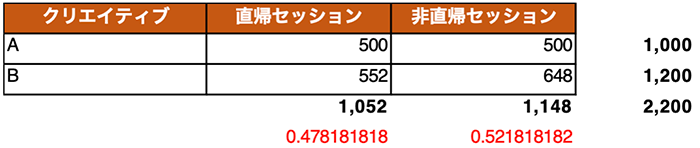
③ 期待値(理論値とも言う)の表の作成
次に、「もし、クリエイティブにかかわらず、直帰、非直帰が0.4782、0.5218の率で発生するとしたら、クリエイティブそれぞれでどんな直帰セッション、非直帰セッションが発生するか?」を示す表を作ります。

太字で表した周辺度数はカイ二乗値の計算のためには不要ですが、検算のために追加しています。
④ カイ二乗値の計算
エクセルの関数は CHISQ.TEST(実測値の表の範囲, 理論値の表の範囲) の形式で利用します
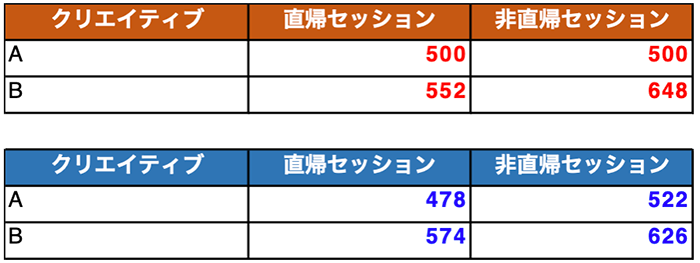
実測値の範囲には、赤の範囲を、期待値の範囲には青の範囲をそれぞれ指定します。意味合い的には、もしクリエイティブによって直帰率に差がないのなら、青の数字になるべきところ、実際には赤であった。ということになります。
計算は一瞬で終わりますが、内部的には以下を行っています。
- 期待値と実測値の差からカイ二乗値を求める(この値は期待値と実測値の差が大きければ大きいほど大きくなります。)
- 要素の数マイナス1で求められる自由度のカイ二乗分布に内部的に取り出したカイ二乗値を照らし合わせる
- その大きさのカイ二乗値がその自由度のもとで発生する確率をP値として出力する
実際に手を動かしてみると、CHISQ.TEST関数は 0.061 を返します。0.05より大きいため、「このくらいのカイ二乗値が取り出せることはままある」、したがって、「クリエイティブは直帰率とは独立」。つまり、クリエイティブにより直帰率に差があるとは言えない。という結論となりました。
エクセルによるカイ二乗検定 – まとめ
如何でしたか?
以下の感想を持つ方が多いのではないでしょうか?
- 実測値と期待値の差に基づき統計的に有意かどうかを判断する考え方は面白い
- ただ、実際にP値をエクセルで取り出すのは面倒
Exploratoryの登場
そこで、Exploratory(エクスプロラトリーと発音します。)の登場です。
Exploratoryはシリコンバレー初の統計的検定、機械学習を組み込んだデータの可視化製品です。開発は日本人が行っています。
特徴としては、データラングリング(データの加工整形)、データの可視化、統計的検定、機械学習を行うエンジンとしてR言語を採用しているところです。Rの持つ世界的なライブラリ開発の力を、使いやすいユーザーインターフェースでユーザーに提供してくれます。
同じデータを使って、Exploratoryであれば、カイ二乗検定がどのように実行できるのかを示します。
Exploratoryによるカイ二乗検定 – データの読み込み
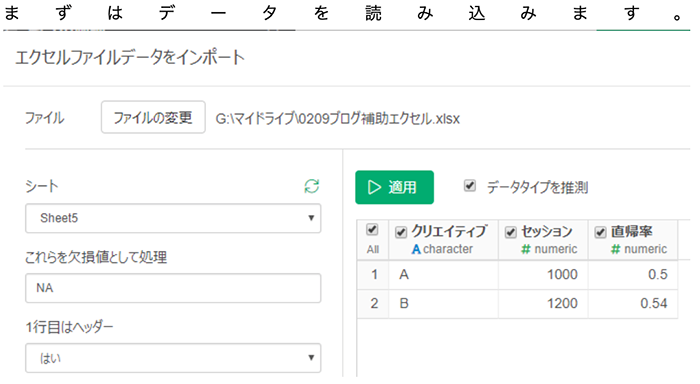
Exploratoryによるカイ二乗検定 – データの整形1
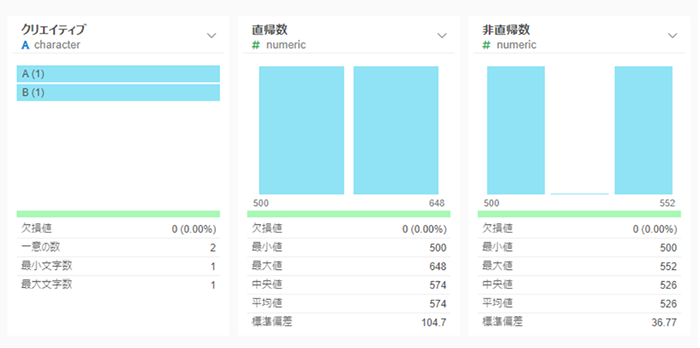
セッション * 直帰率で「直帰数」を求め列を増やします。
セッション – 直帰数で「非直帰数」を求め、列を増やします
Exploratoryによるカイ二乗検定 – データの整形2
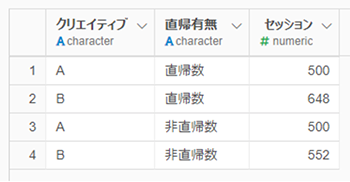
横縦変換を掛けて、このような形にします。意味している内容が元データからは変わっていないことが確認できます。
Exploratoryによるカイ二乗検定 – 設定
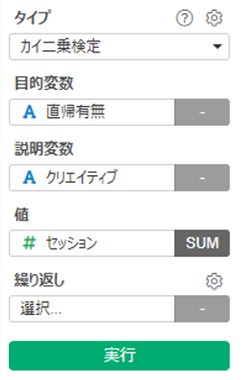
タイプに「カイ二乗検定」を選択し、目的変数、説明変数、セッションを選びます。
Exploratoryによるカイ二乗検定 – 結果
実行ボタンをクリックすると、一瞬で以下の結果が得られます。

当たり前と言えば当たり前ですが、エクセルと同じP値が得られ、クリエイティブと直帰率は独立という結論に至ります。
また、エクセルでは取り出せなかった、カイ二乗値、自由度、効果量、検出力、タイプ2エラーの確率などP値以外の情報も同時に出力されます。
Exploratoryによるカイ二乗検定 – まとめ
Exploratoryに多少の習熟は必要なものの、エクセルよりも断然素早くカイ二乗検定を行うことができました。
しかし、Exploratoryが素晴らしいのはここからです。我々が取り扱うデータは、実際にはこんな形をしていることが多いですね。
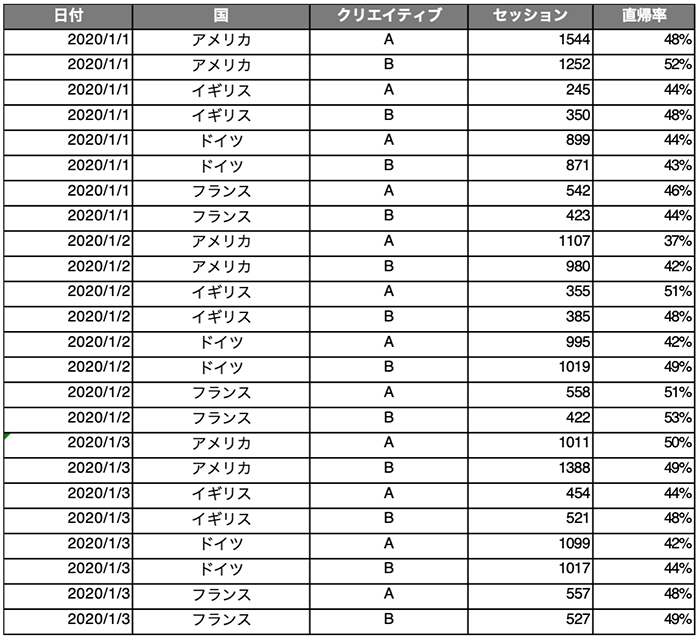
そんなデータでもExploratoryは高いデータ整形力で、1、2分で以下のようなテーブルにデータを整形できます
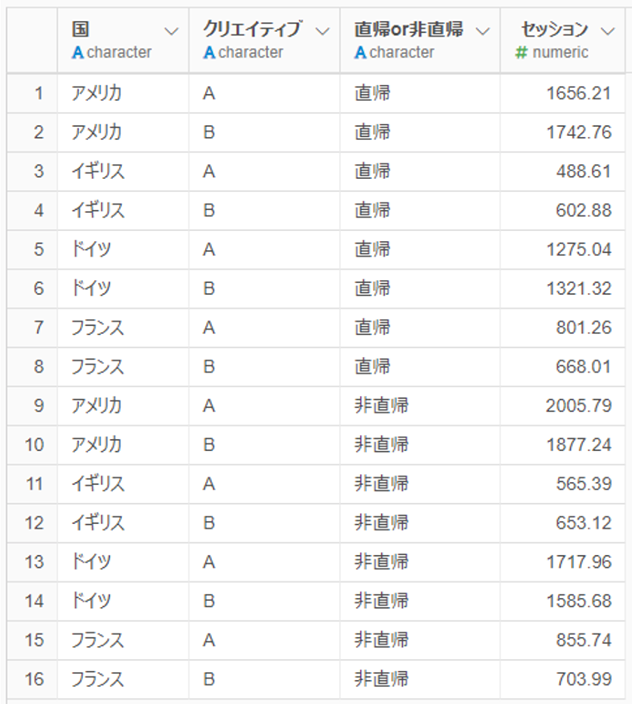
また、同じ計算を任意のディメンションで繰り返し実行する「繰り返し」という機能があります。「国」に沿って繰り返し計算をさせると、瞬時に、以下のようなデータを取り出すことができます。

アメリカとドイツにおいては、P値が0.05以下であるため、「クリエイティブの種類と直帰率が独立である」という帰無仮説が棄却され
クリエイティブは直帰率に影響している
と言えます。
まとめ
Web解析にこれまであまり統計学的なアプローチが取られてこなかった理由と、統計学的なアプローチが必要になるケースをWeb解析と統計学的アプローチという記事にまとめていますので、そちらも併せてご参照ください。








