データ処理速度を爆速にするアルゴリズム最適化の例

はじめに：データ処理速度は現代の重要課題

と悩んでいませんか？

2010年頃に「ビッグデータ」という言葉が世の中に出てから、およそ10年が経ちました。日々データを扱う方々は、膨大な量のデータ処理に労力と時間をかけていることかと思います。

では、どうすれば処理速度を上げることができるのでしょうか。

処理速度は、データ処理の方法に大きく依存します。本記事では、アルゴリズムを改良することで処理速度が上がる1つの例として、トリボナッチ数列の処理を行います。

トリボナッチ数列自身はマーケティングの現場では使われませんが、この記事が処理方法を見直すきっかけとなり、負担が軽減すれば幸いです。

データ構造とアルゴリズムは処理速度を左右する

データ構造によって処理速度は異なる

データ構造を最適化すると、データ処理を高速化できます。

データ構造とは、コンピュータの内部で効率的に処理するために、データの集合を系統立てて管理する形式のことです。スタック、キュー、リストなどがデータ構造を学び始めた時に目にする代表例でしょうか。

アルゴリズムによって処理速度は異なる

アルゴリズムを最適化すると、データ処理を高速化できます。

ここでいうアルゴリズムとは「データを処理する手順」のことです。同じ結果になる処理であっても、その手順により効率が異なるのです。

例えば、5人の学生が受けたテストの点数から、上から3つの点数を探すとします。この場合、3つのアルゴリズムがあります。

点数例: 90, 12, 45, 66, 81, 77

アルゴリズム1: 1番高い点数を3回探索する

1. 5つの点数を配列に格納し、一番高い点数を取得する -> 90
2. 90点を除いた残り4つの点数を全て確認し、再び1番高い点数を取得する -> 81
3. 81点を除いた残り3つの点数を全て確認し、再び1番高い点数を取得する -> 77

アルゴリズム2: 並び替え、上から3つを取得する

1. 配列に格納し、降順に点数を並び替える -> [90, 81, 77, 66, 45, 12]
2. 上から3つの点数を取得する -> 90, 81, 77

(ソートにも様々な方法があるので、ソート アルゴリズムをどうするか？という話は生まれます)

アルゴリズム3: 各点数ごとの人数をカウントする

1. 点数pをマークした人数を、配列C[p]に格納する
   -> C[100] = 0, C[99] = 0, …, C[90] = 1, …, C[81] = 1, …,C[0] = 0
2. C[100], C[99], …, C[0]の順にC[p]が1以上の場合、pをC[p]回取得する(合計3回まで)
   -> C[90] = 1, C[81] = 1, C[77] = 1
   -> 90, 81, 77

これらのアルゴリズムは、どれか1つが絶対的に優れているわけではありません。最適なアルゴリズムは処理対象のデータ数などにより変わってきます。

今回は5つの点数しかないので、アルゴリズム1でも計算量は無視できます。ただし、データ数が増えると、同時に計算量も多くなってしまいます。

アルゴリズム2はまずソートして、その後に上位N個の点数を取得する点で、取得する点数が増えても、計算量がそれに比べて増えにくいと言えるでしょう。

アルゴリズム3はテストの点数はここでは取りうる値が0 ~ 100に限られているため、計算効率はよさそうです。ですが範囲が非常に大きくなると、必要な記憶容量も膨大になるため、実用向けではありません。

上記のテストの例では取りうる値と値の個数は非常に限られています。ですが、ECサイトの購買データのような膨大な商品数や価格、販売個数があるようなデータだったら、いかがでしょうか。

このように、目的を達成するための手順によって、大きな処理速度の違いが発生します。

アルゴリズムの改良による高速化の例

実際にデータ構造を見直し、アルゴリズムの改良によって、処理速度が速くなる例を確認してみましょう。

今回はトリボナッチ数列を列挙するプログラムを、メモ化によって速度改善を図ります。メモ化とはプログラム高速化のための1つの手法であり、呼び出した処理の結果を保存して計算量を大幅に削減するものです。

（前述のとおり、トリボナッチ数列はマーケティングの現場で使われるものではありません。あくまでデータ処理高速化の例です。）

またプログラムはJavaScript を使用します。

環境情報

$ cat /etc/os-release
> NAME="Ubuntu"
> VERSION="18.04.3 LTS (Bionic Beaver)"

$ node -v
> v10.14.2

比較する指標

トリボナッチ数列は以下の漸化式で定義されます。

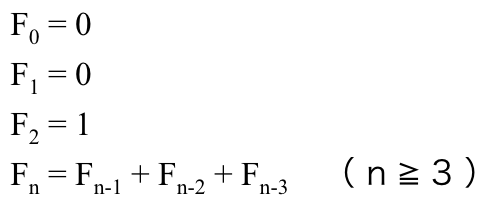
上記を実数で表すと、以下のような数列です。
0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81, 149, 274, …

今回はこのトリボナッチ数列を「40番目まで計算する時間」を指標に、2つのアルゴリズムを比較します。

アルゴリズム1: 愚直に計算

まずは愚直に計算するアルゴリズムで処理します。プログラムは以下のようになります。

'use strict';

function calcTrib(n) {
	if (n === 0 || n === 1) {
		return 0;
	} else if (n === 2) {
		return 1;
	} else {
		return calcTrib(n - 1) + calcTrib(n - 2) + calcTrib(n - 3);
	}
}

関数calcTrib は引数nを受け取り、トリボナッチ数列におけるn番目の値を返却します。

0番目、1番目の場合は共に0、 2番目は1を計算せず返却します。それ以外ではcalcTribを関数内で呼び出す再帰処理をしています。

40番目までの値を出力する処理の時間を、time コマンドで計測すると以下のようになります。

const MAX = 40;
for (let i = 0; i < MAX; i++) {
	console.log(calcTrib(i));
}

$ time node main.js
> real 1m57.041s
> user 1m56.898s
> sys 0m0.046s

上記は、起動から終了までにかかった時間は1分57.041秒、プログラムがCPUを使った時間は1分56.898秒であったことを示します。

体感的には実行中、後の計算結果になるほど算出に時間がかかり、非常にストレスフルです。

アルゴリズム1の計算に時間がかかる理由

n番目が増えれば増えるほど、計算量が爆発的に増えていきます。なぜなら、漸化式を毎回初めから計算しているからです。

x軸にn番目、y軸に計算回数をとってグラフ化すると、以下のようになります。

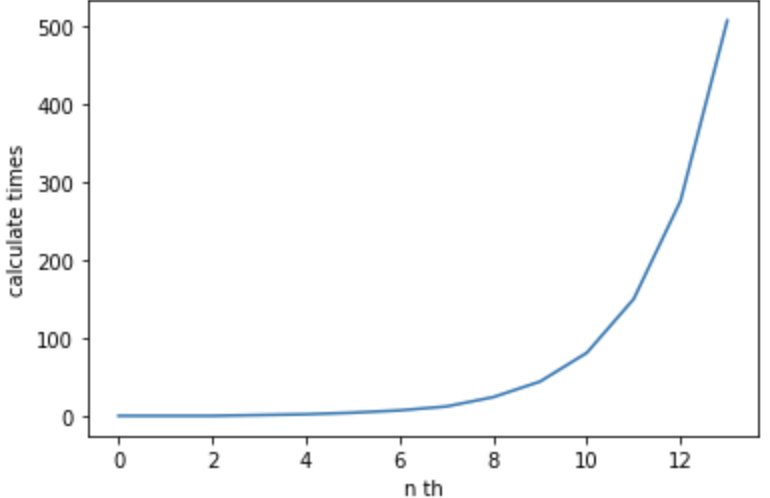
このように、13番目までであっても、爆発的に計算量が増えています。これ以降の計算回数の増加スピードは、nの増加量に比べて、圧倒的に加速していきます。その結果、処理の時間が非常に長い時間がかかったり、現実的な時間では終了しない事態になります。

アルゴリズム2: メモ化して計算結果を保存し、再計算を防ぐ

それでは一度計算したことがある結果を保存（メモ化）して、計算する回数を減らす方法を実行してみます。

Map オブジェクトを使い、メモ化でアルゴリズムを改善してみます。Map オブジェクトとは、キーと値のペアを保持し、キーが最初に挿入された順序を保持するものです。

今回では、キーをn番目の数値、値をn番目のトリボナッチ数列での値で保持します。

以下のような構造になっていきます。
{ 0: 0, 1: 0, 2: 1, 3: 2, 4: 4, 5: 7, 6: 13, 7: 24, 8: 44, 9: 81, 10: 149, …, n: 番目の数値 }

アルゴリズム2の手順

1. 保持用のmap を作成する
2. map に0, 1, 2番目の値をset する
3. map が引数n をキーとした値を持っていれば返却し、なければ再帰的に計算してmap にセットした上で値を返却する

コードは以下です。

'use strict';

let memo = new Map();
memo.set(0, 0);
memo.set(1, 0);
memo.set(2, 1);

function calcTribWithMemo(n) {
	if (memo.has(n)) {
		return memo.get(n);
	}

	const value = calcTribWithMemo(n - 1) + calcTribWithMemo(n - 2) + calcTribWithMemo(n - 3);
	memo.set(n, value);
	return value;
}

const MAX = 40;
for (let i = 0; i < MAX; i++) {
	console.log(calcTribWithMemo(i));
}

再度、time コマンドで実行した結果は以下でした。

$ time node main.js
> real 0m0.066s
> user 0m0.039s
> sys 0m0.017s

愚直に計算したアルゴリズム1では、realが 1m57.041s、userが1m56.898sだったので、圧倒的に計算が速くなったことがおわかりいただけると思います。

• real 1m57.041s → 0m0.066s
• user 1m56.898s → 0m0.039s

n番目が増えれば増えるほど、再計算する必要があった箇所を、メモの中に保持して再利用するようにしました。その結果、計算量が減ったため、処理時間が短縮されました。

まとめ

この記事では、処理速度を向上させるための方法として、データ構造およびアルゴリズムの改良を紹介しました。トリボナッチ数列の例では、データ構造とアルゴリズムを変えると処理時間が大幅に削減されました。

改良の際に重要なのは、現状の処理のうち、どこに時間がかかっているか？を把握することです。つまり、処理のボトルネックを見つけ、重点的に解決することが高速化への近道です。

この記事が処理方法を見直すきっかけになれば幸いです。

また、弊社ではデータを活用したマーケティング戦略の立案から実行までを支援させていただいております。なにかお役立ちさせていただけることがあれば幸いです。お気軽に弊社窓口よりお問い合わせください。